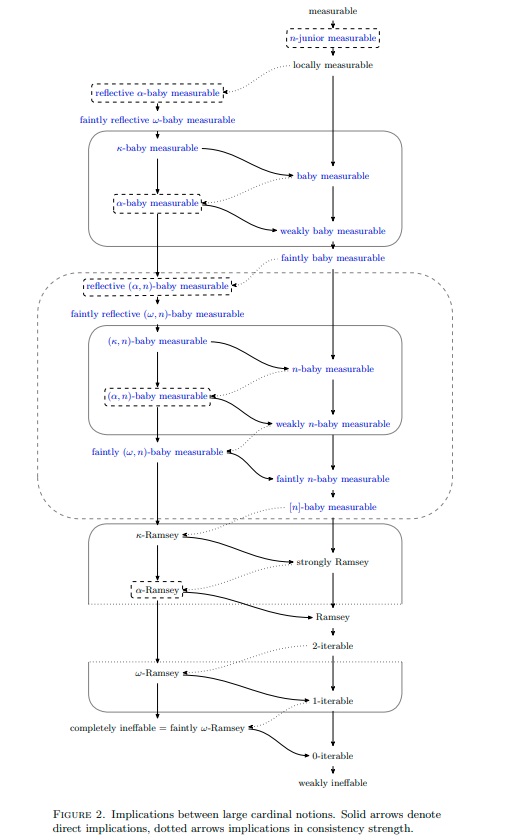
New large cardinal chart of Ramsey-like cardinals
In our article "Between Ramsey and Measurable cardinals" with Philipp Schlicht [1] (see this post), we explored new large cardinal hierarchies between Ramsey and measurable cardinals. Most large cardinal notions $\kappa$ below a measurable cardinal are defined via the following template: for every $A\subseteq \kappa$, there is a transitive model $M$ of size $\kappa$ satisfying ${\rm ZFC}^-$ (${\rm ZFC}$ without powerset) with $V_\kappa\cup\{\kappa\}\subseteq M$ for which there is a (uniform) filter $U$ measuring all subsets of $\kappa$ in $M$ that is normal for $\kappa$-length sequences from $M$ and satisfies some additional niceness properties (e.g. the ultrapower by $U$ is well-founded, $U$ is amenable to $M$, $U$ is iterable, the intersection of any countable collection of elements of $U$ has a non-empty intersection, etc.) While in this scheme, $M$ is a model of the ${\rm ZFC}$ axioms without powerset (and often a model of full ${\rm ZFC}$), the ${\rm ZFC}$ axioms can fail very badly in the structure $\langle M,\in, U\rangle$ together with a predicate for $U$. It turns out that the larger the fragment of ${\rm ZFC}^-$ that the structure $\langle M,\in, U\rangle$ satisfies the stronger the large cardinal axiom given by the above characterization. If $\kappa$ is weakly compact, then the structures $\langle M,\in, U\rangle$ may not even satisfy $\Sigma_0$-separation. If the structures $\langle M,\in, U\rangle$ satisfy $\Sigma_0$-separation, even if the ultrapower is not guaranteed to be well-founded, we get a large cardinal that is larger than a weakly ineffable and consistency-wise stronger than an ineffable. If the structures $\langle M,\in, U\rangle$ satisfy $\Sigma_0$-separation and $\Sigma_0$-collection, we get a large cardinal notion that is much stronger than Ramsey, and, so, in particular, outside of $L$. Some of the new large cardinal notions in this chart arise from considering the characterizations where the structures $\langle M,\in, U\rangle$ satisfy larger and larger fragments of ${\rm ZFC}^-$. Others arise from combining the existence of strong structures $\langle M,\in, U\rangle$ with with game-theoretic properties introduced by Peter Holy and Philipp Schlicht in [2].
References
- V. Gitman and P. Schlicht, “Between Ramsey and measurable cardinals,” Manuscript, 2023.
- P. Holy and P. Schlicht, “A hierarchy of Ramsey-like cardinals,” Fund. Math., vol. 242, no. 1, pp. 49–74, 2018.
