Between Ramsey and measurable cardinals

PDF   Bibtex   Arχiv

V. Gitman and P. Schlicht, “Between Ramsey and measurable cardinals,” Manuscript, 2023.

Measurable cardinals and most stronger large cardinals are defined by the existence of elementary embeddings $j:V\to M$ from the universe $V$ into an inner model $M$ with that cardinal as the critical point. Stronger large cardinal axioms impose additional assumptions on the target model $M$ that allow it to capture more and more sets from $V$. Weakly compact and many other smaller large cardinals are defined via combinatorial properties, often involving existence of large homogeneous sets for colorings. But almost all of them also have elementary embedding characterizations that, like the larger large cardinals, follow prescribed patterns as consistency strength grows. These smaller large cardinals $\kappa$ are characterized by elementary embeddings of models $\langle M,\in\rangle\models{\rm ZFC}^-$ of size $\kappa$, most often transitive, with critical point $\kappa$, and usually, but not always, with well-founded targets. ${\rm ZFC}^-$ is the theory ${\rm ZFC}$ with the powerset axiom removed, the collection scheme in place of the replacement scheme, and the version of the axiom of choice which states that every set can be well-ordered.(Without the powerset axiom, collection and replacement schemes are not equivalent and neither are the various forms of the axiom of choice. See [1] and [2].) In many cases, the existence of these embeddings can be equivalently expressed in terms of the existence of certain ultrafilters on the subsets of $\kappa$ contained in $M$.

Suppose $\langle M,\in\rangle \models{\rm ZFC}^-$ is a transitive model of size $\kappa$ with $\kappa\in M$. We call such structures weak $\kappa$-models. We will call a filter $U$, on the subsets of $\kappa$ of a weak $\kappa$-model $M$, an $M$-ultrafilter if the structure $\langle M,\in,U\rangle$, together with a predicate for $U$, satisfies that $U$ is a uniform, normal ultrafilter on $\kappa$. What this says is that $U$ is an ultrafilter on the subsets of $\kappa$ that live in $M$ and if a $\kappa$-length sequence of elements of $U$ is an element of $M$, then its diagonal intersection is in $U$. Łoś' Theorem holds for ultrapowers by an $M$-ultrafilter, but the ultrapower need not be well-founded. Note that the filter $U$ may not be countably complete for sequences outside of $M$. The $M$-ultrafilter $U$, is in most interesting cases, external to $M$ and even though $\langle M,\in\rangle\models{\rm ZFC}^-$, separation and replacement can fail completely in the structure $\langle M,\in,U\rangle$ once we let $M$ know about $U$. In the same way that making the inner model $M$ closer to $V$ in the characterizations of larger large cardinals increases strength, for the smaller large cardinals, we increase strength by making $M$ be more compatible with $U$, which amounts to $M$ being more correct about the properties of $U$ or to having more of the ${\rm ZFC}^-$ axioms in the structure $\langle M,\in,U\rangle$.

Let's look at some examples. A cardinal $\kappa$ is weakly compact if and only if it is inaccessible and every $A\subseteq\kappa$ is an element of a weak $\kappa$-model $M$ for which there is an $M$-ultrafilter with a well-founded ultrapower. It turns out that it is equivalent to assume the a priori stronger assertion that every $A\subseteq \kappa$ is an element of a weak $\kappa$-model for which there is a (externally) countably complete $M$-ultrafilter $U$. In particular, the ultrapower is well-founded. A cardinal $\kappa$ is $1$-iterable if every $A\subseteq\kappa$ is an element of a weak $\kappa$-model $M$ for which there is an $M$-ultrafilter $U$ such that $\la M,\in, U\ra$ satisfies $\Sigma_0$-separation and the ultrapower is well-founded [3]. The $1$-iterable cardinals are stronger than ineffable cardinals, and therefore much stronger than weakly compact cardinals. They are however still compatible with $L$. Thus, the additional requirement that the structure $\langle M,\in, U\rangle$ satisfies $\Sigma_0$-separation pushes up the consistency strength. A cardinal $\kappa$ is Ramsey if and only if every $A\subseteq\kappa$ is an element of a weak $\kappa$-model $M$ for which there is an $M$-ultrafilter $U$ such that $\langle M,\in,U\rangle$ satisfies $\Sigma_0$-separation and which is (externally) countably complete [4]. Ramsey cardinals sit much higher in the hierarchy than $1$-iterable cardinals. Thus, in particular, in the presence of the requirement of $\Sigma_0$-separation for the structure $\langle M,\in, U\rangle$ for the $M$-ultrafilter $U$, having $U$ be countably complete is much stronger than having it just produce a well-founded ultrapower.

In this article, motivated by the work of Bovykin and McKenzie [5], we consider a hierarchy of large cardinal notions characterized by the existence, for weak $\kappa$-models $M$, of $M$-ultrafilters $U$ such that the structure $\langle M,\in,U\rangle$ satisfies fragments up to full ${\rm ZFC}^-$. Following Bovykin and McKenzie, we call such cardinals $n$-baby measurable where the fragment is ${\rm ZFC}^-_n$ (the separation and collection schemes are restricted to $\Sigma_n$-formulas). Baby measurable cardinals and some variants were introduced by Bovykin and McKenzie in [5] and used to obtain the following application to the theory ${\rm NFUM}$. This theory is a natural strengthening of ${\rm NFU}$ due to Holmes (see [5]) that aims to facilitate mathematics in ${\rm NFU}$, the latter being a variant of Quine's New Foundations with Urelements introduced by Jensen.

Theorem: (Bovykin, McKenzie [5]) The following theories are equiconsistent.

We show in that increasing levels of collection and separation for the structures $\langle M,\in,U\rangle$ increase the large cardinal strength. For example, adding even $\Sigma_0$-replacement to the characterization of $1$-iterable cardinals pushes consistency strength well beyond a Ramsey cardinal, and hence beyond $L$. We then provide a fine analysis of the resulting hierarchies. Surprisingly, the closure of the models does not play a role when working solely with fragments of collection. However, closure conditions do induce a strict hierarchy for the setting of ${\rm ZFC}^-_n$ with both the collection and separation schemes restricted to $\Sigma_n$-formulas. We show this with the help of filter games resembling those introduced by Holy and the second-listed author [6]. We thus arrive at similar patterns of large cardinal notions as the one around strongly Ramsey cardinals.

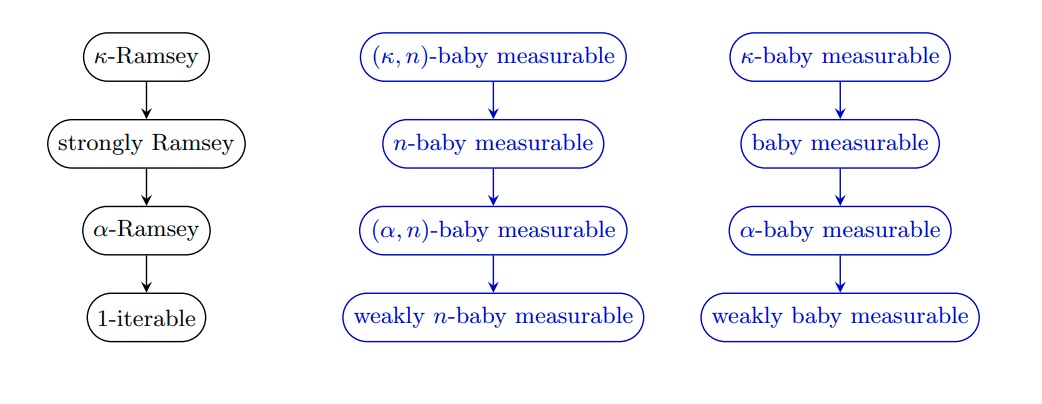
We show that some of these new large cardinal notions are robust under forcing. Finally, we will see that these notions are naturally connected to models of Kelley-Morse set theory in which ${\rm Ord}$ is measurable and help us to understand the structure of these second-order models. In particular, we apply the above methods to show that the theory of structures of the form $V_\kappa^M$, where $M$ is a model of ${\rm ZFC}^-$ or ${\rm ZFC}$ where $\kappa$ is measurable, is axiomatizable by the existence of large cardinals similar to the ones above. These results shed light on the large cardinal hierarchy below measurable cardinals and provide a blueprint how to approximate a large cardinal notion from below by a natural hierarchy.

References

  1. A. Zarach, “Unions of ${\rm ZF}^{-}$-models which are themselves ${\rm ZF}^{-}$-models,” in Logic Colloquium ’80 (Prague, 1980), vol. 108, Amsterdam: North-Holland, 1982, pp. 315–342.
  2. V. Gitman, J. D. Hamkins, and T. A. Johnstone, “What is the theory $\mathsf {ZFC}$ without power set?,” MLQ Math. Log. Q., vol. 62, no. 4-5, pp. 391–406, 2016.
  3. V. Gitman and P. D. Welch, “Ramsey-like cardinals II,” The Journal of Symbolic Logic, vol. 76, no. 2, pp. 541–560, 2011.
  4. W. Mitchell, “Ramsey cardinals and constructibility,” J. Symbolic Logic, vol. 44, no. 2, pp. 260–266, 1979.
  5. A. Bovykin and Z. McKenzie, “Ramsey-like cardinals that characterize the exact consistency strength of NFUM,” Manuscript.
  6. P. Holy and P. Schlicht, “A hierarchy of Ramsey-like cardinals,” Fund. Math., vol. 242, no. 1, pp. 49–74, 2018.